
For these points the function f is non-differentiable. Thus, equations of the tangents to graphs of all these functions, as well as many others, can be found by the methods of calculus.Ĭalculus also demonstrates that there are functions and points on their graphs for which the limit determining the slope of the tangent line does not exist. The technique of adequality is similar to taking the difference between f ( x + h ) Ĭalculus provides rules for computing the derivatives of functions that are given by formulas, such as the power function, trigonometric functions, exponential function, logarithm, and their various combinations. In the 1630s Fermat developed the technique of adequality to calculate tangents and other problems in analysis and used this to calculate tangents to the parabola. 212 BC) found the tangent to an Archimedean spiral by considering the path of a point moving along the curve. 225 BC) he defines a tangent as being a line such that no other straight line couldĪrchimedes (c. The word "tangent" comes from the Latin tangere, "to touch".Įuclid makes several references to the tangent ( ἐφαπτομένη ephaptoménē) to a circle in book III of the Elements (c. The concept of a tangent is one of the most fundamental notions in differential geometry and has been extensively generalized see Tangent space. Similarly, the tangent plane to a surface at a given point is the plane that "just touches" the surface at that point.

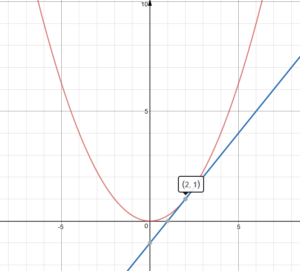
The tangent line to a point on a differentiable curve can also be thought of as a tangent line approximation, the graph of the affine function that best approximates the original function at the given point. A similar definition applies to space curves and curves in n-dimensional Euclidean space.Īs it passes through the point where the tangent line and the curve meet, called the point of tangency, the tangent line is "going in the same direction" as the curve, and is thus the best straight-line approximation to the curve at that point. More precisely, a straight line is said to be a tangent of a curve y = f( x) at a point x = c if the line passes through the point ( c, f( c)) on the curve and has slope f '( c), where f ' is the derivative of f.

Leibniz defined it as the line through a pair of infinitely close points on the curve. It is denoted as tanθ, where θ is the angle between the two sides.In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. The sign is a trigonometric function of an angle. The tangent function is defined as the ratio of the length of the opposite side to that of the length of the adjacent side in a right-angled triangle. Step 3: Click on the "Reset" button to clear the fields and find the tangent value for the different angles.Step 2: Click on the "Calculate" button to find the tangent value for a given angle theta.Step 1: Enter the angle theta (in degrees) in the given input box.Please follow the steps below to find the tangent value for a given angle theta: NOTE: Enter angle theta between -360° to 360° only. 'Tangent Calculator' is an online tool that helps to calculate the tangent value for a given angle theta. This Tangent Calculator helps you to calculate the tangent value for a given angle theta in a few seconds. The tangent line in calculus may touch the curve at any other point(s) and it also may cross the graph at some other point(s) as well. The tangent line of a curve at a given point is a line that just touches the curve ( function) at that point. Tangent is defined as a line or plane that intersects a curve or a curved surface at exactly one point.


 0 kommentar(er)
0 kommentar(er)
